1

Note interval | Minor and Major Intervals | Intervals

You can watch this lesson in the video below, or read at your ease under the video.

When you play 2 different notes at the same time or one after the other, you will have a lower and a higher note. This means there is a distance (in pitch) between the 2 notes. This distance is called the interval between the 2 notes, the note interval, or simply interval.

You can measure this intervals between notes in number of semitones, and this takes us directly to our first interval: the semitone.

The semitone

The easiest way to explain semitones is to look at the piano keyboard. A semitone is the interval from a key on the keyboard to the first note at the left or the right. So, for example, the interval from C to C# (or Db) in the next figure is a semitone.

Or, for example from G# (or Ab) to A:

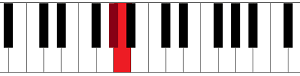
It’s also possible to have a semitone between 2 white keys; this is the case between E and F and between B and C:

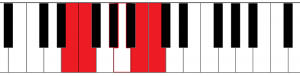
Notice that it’s not possible to have an interval of a semitone between 2 black keys on the piano.

Other names for a semitone are: half tone or half step.

The whole tone

The whole tone, or also called whole step, is an interval that consists of 2 semitones. Here are some examples of a whole tone:

From C to D:

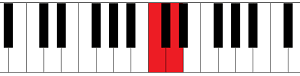
From F# (or Gb) to G# (or Ab):

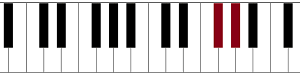
From E to F# (or Gb):

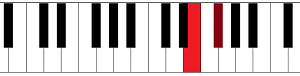
From Bb (or A#) to C:

 

Intervals from C to other ‘white key-notes’

Let’s take a look at the intervals from C to the other white keys on the piano up till the next C. Those notes are the notes from the C major scale (as you will learn later).

• When we call C the first note, D the second note, E the third note and so on, then the interval from C to the second note (D) is simply called ‘second’. The interval from C to the third note (E) is called ‘third’. And so on…
• The interval from C to the eighth note (C) is not called ‘eighth’, but ‘octave’.
• The interval from C to itself is called ‘’unison’.

In the table below, you can see an overview of all those intervals:

Note 1: the interval from C to D is not called ‘whole tone’ in this table, because ‘whole tone’ is actually an alternative name, where ‘second’ is more an official name. However, ‘whole tone’ is used more often than ‘second’.

Note 2: it might seem strange to call the unison an interval, since there is no distance between a note and itself. You could however call this a distance of 0 (semitones).

Interval on piano keyboard:	Interval between the notes:	Distance in (whole) tones:	Name of the interval:
	C-C	0	unison
	C-D	1	second
	C-E	2	third
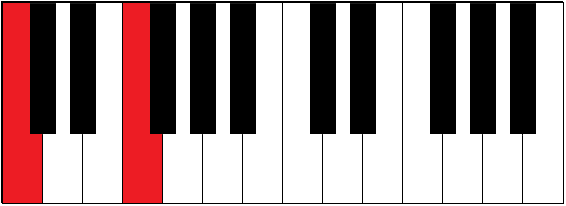	C-F	2½	fourth
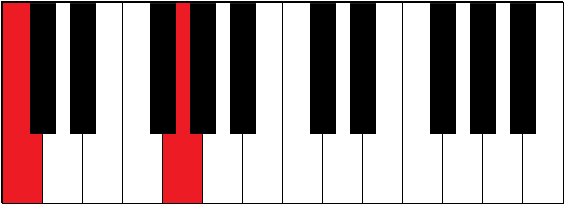	C-G	3½	fifth
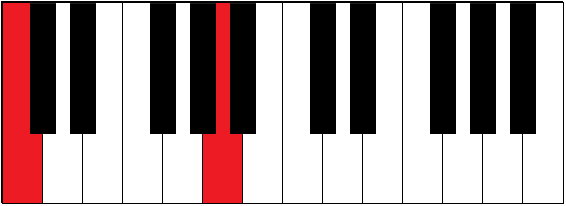	C-A	4½	sixth
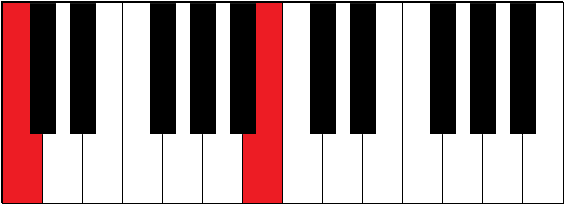	C-B	5½	seventh
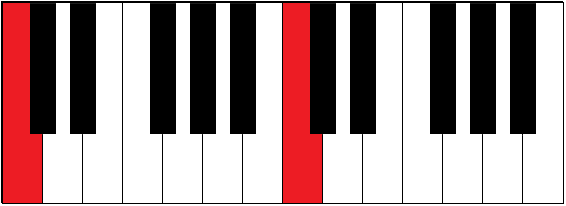	C-C	6	octave

 

All the intervals from C

Let’s also include in the table the intervals from C to the notes on black keys on the piano.

To do so, we have to introduce perfect intervals, major intervals and minor intervals.

Actually, in the table above, the unison, the fourth, the fifth and the octave are all perfect intervals. So, we speak of the perfect unison, the perfect fourth, and so on (even if we often omit the term ‘perfect’, and we just say unison, fourth, … etcetera).

All the other intervals in the table above are major intervals, so: major second, major third, major sixth and major seventh. The minor intervals will appear between C and the ‘black notes’ (table below).

In order to complete the table below, we have to follow the next rules:

• When a major interval is reduced by a half tone, it becomes a minor interval (this is not possible for a perfect interval). For example, when a major 3^rd interval (C-E) is reduced by a half tone, it becomes a minor 3^rd interval (C-Eb).
• Perfect intervals and minor intervals can be reduced by a half tone, they then become diminished intervals. For example, when a perfect 5^th (C-G) is reduced by a half tone, it becomes a diminished 5^th (C-Gb).
• Perfect intervals and major intervals can be increased by a half tone, they then become augmented intervals. For example, when a perfect 5^th (C-G) is increased by a half tone, it becomes an augmented 5^th (C-G#).

The table below can be scrolled horizontally (under the table).

Interval on piano keyboard:	Interval between the notes:	Distance in number of (whole) tones	Interval name (perfect/major/minor):	Interval name (diminished/ augmented):	Alternative name(s):
	C-C	0	perfect unison
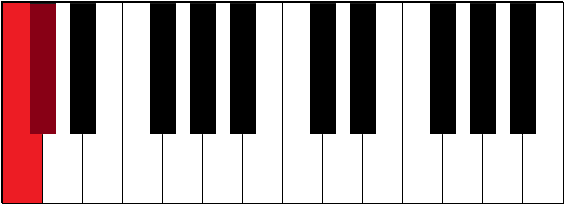	C-C#	½		augmented unison	half tone, semitone, half step
	C-Db	½	minor second		half tone, semitone, half step
	C-D	1	major second		whole tone, whole step
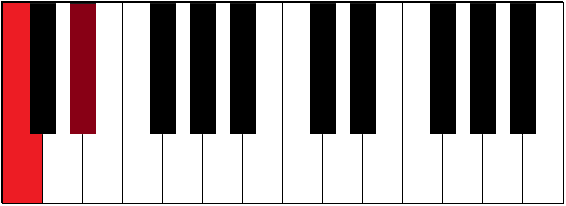	C-D#	1½		augmented second
	C-Eb	1½	minor third
	C-E	2	major third
	C-F	2½	perfect fourth
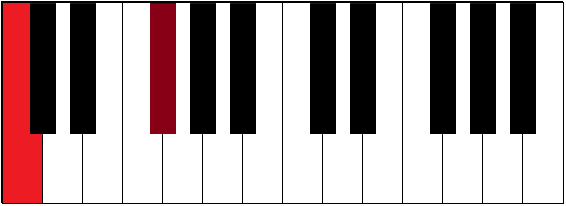	C-F#	3		augmented fourth	tritone
	C-Gb	3		diminished fifth	tritone
	C-G	3½	perfect fifth
	C-G#	4		augmented fifth
	C-Ab	4	minor sixth
	C-A	4½	major sixth
	C-A#	5		augmented sixth
	C-Bb	5	minor seventh
	C-B	5½	major seventh
	C-C	6	perfect octave

Now, I can imagine that all this looks quite difficult, especially when you’re a beginner and you see all those interval names for the first time.

In that case: don’t worry: we will, especially in the beginning, not use all those interval names. So don’t start learning the table above by heart, but limit yourself to the next intervals:

• Half tone (also called: semitone or half step)
• Whole tone
• Minor 3^rd
• Major 3^rd
• Perfect 4^th
• Perfect 5^th
• Major 6^th
• Minor 7^th
• Major 7^th
• Perfect octave

And, as I said before, I normally speak of the 4^th, 5^th and octave and not of perfect 4^th, perfect 5^th and perfect octave.

When you start learning about diminished chords, you should also know what a diminished 5^th and a diminished 7^th is, but that’s for later…

Note: We normally call the notes after their interval they make with the root (the root is the starting note, in our example the root is the note C (you will learn more about this in the major scales)). So, when the root is C, then the note E is called the major 3^rd. So, ‘major 3^rd’ is then not only the name of the interval (from C to E), but also of the note E (but only when the root is C!).

Intervals from another root note than C

Till now, we’ve only seen the intervals in the C major scale, so intervals from the root note C. How does this work in other major scales, or said in another way: how does this work from another root note than C?

Let me take as an example the root note G. So, we’re then looking for all the intervals from G to other (white and black) notes up till the next G an octave higher.

When you already know how major scales ‘work’, you can simply look at the G major scale: from G to the second note of the G major scale (A) is the major 2^nd, from G to the third note of the G major scale the major 3^rd, to the fourth note the perfect 4^th, and so on… Watch out: the major 7^th is now on a black key, the F#.

When you still don’t know how major scales ‘work’, then just look at the number of tones in the second table and apply that from the note G.

The result is shown in the table below:

The table below can be scrolled horizontally (under the table).

Interval on the piano keyboard:	Interval between the notes:	Distance in number of (whole) tones:	Interval name (perfect/major/minor):	Interval name (diminished/ augmented):	Alternative name:
	G-G	0	perfect unison
	G-G#	½		augmented unison	half tone, semitone, half step
	G-Ab	½	minor second		half tone, semitone, half step
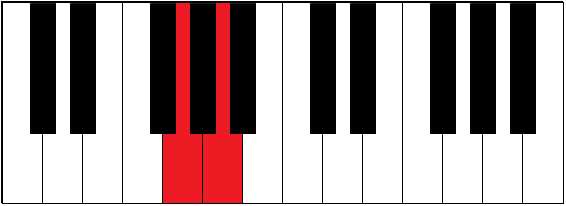	G-A	1	major second		whole tone, whole step
	G-A#	1½		augmented second
	G-Bb	1½	minor third
	G-B	2	major third
	G-C	2½	perfect fourth
	G-C#	3		augmented fourth	tritone
	G-Db	3		diminished fifth	tritone
	G-D	3½	perfect fifth
	G-D#	4
	G-Eb	4	minor sixth
	G-E	4½	major sixth
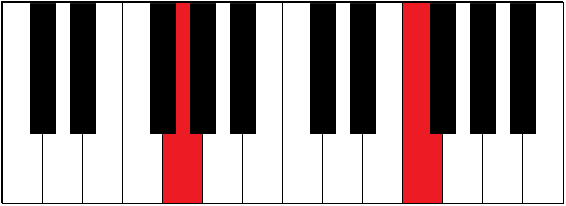	G-E#	5		augmented sixth
	G-F	5	minor seventh
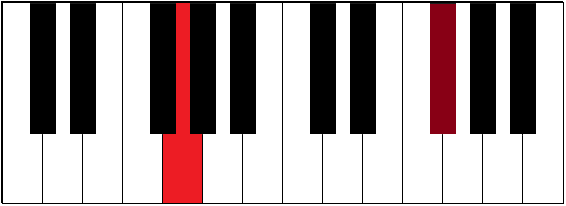	G-F#	5½	major seventh
	G-G	6	perfect octave

One further step

When you’re already more advanced in music (theory) and you want to know more about intervals, then keep reading. When you’re a beginner, then just scroll down to the bottom of this page where you will find interactive exercises about intervals.

In the first lesson (about note names) I told you already something about double sharps and double flats.

As you know, C and Dbb are the same note on the piano. Does this mean that the interval between C and Dbb is the same interval as the interval between C and C, so a unison?

No. The interval from C to Dbb is not called a unison. We call this interval a diminished 2^nd.

But why second? This is because Dbb is based on the note D: it is a D that has been lowered twice by a half tone: From C to D is a major 2^nd, from C to Db a minor 2^nd, so from C to Dbb a diminished 2^nd.

Now, to be honest: you will almost never see the name ‘diminished 2^nd’, but officially it exists.

But, for example a diminished 7^th occurs often in music, for example in the C diminished chord. A diminished 7^th is a half tone lower than a minor 7^th, so a half tone lower than Bb (when C is the root note). This makes the diminished 7^th in the key of C the note Bbb, which is on the piano the same note as the A.

We can now extend our table as follows (from the root C):

The table below can be scrolled horizontally (under the table).

Interval on the piano keyboard:	Interval between the notes:	Distance in number of (whole) tones:	Interval name (perfect/major/minor):	Interval name (diminished/ augmented):	Alternative name:
	C-C	0	perfect unison
	C-Dbb	0		diminished second
	C-C#	½		augmented unison	half tone, semitone, half step
	C-Db	½	minor second		half tone, semitone, half step
	C-D	1	major second		whole tone, whole step
	C-Ebb	1		diminished third	whole tone, whole step
	C-D#	1½		augmented second
	C-Eb	1½	minor third
	C-E	2	major third
	C-Fb	2		diminished fourth
	C-E#	2½		augmented third
	C-F	2½	perfect fourth
	C-F#	3		augmented fourth	tritone
	C-Gb	3		diminished fifth	tritone
	C-G	3½	perfect fifth
	C-Abb	3½		diminished sixth
	C-G#	4		augmented fifth
	C-Ab	4	minor sixth
	C-A	4½	major sixth
	C-Bbb	4½		diminished seventh
	C-A#	5		augmented sixth
	C-Bb	5	minor seventh
	C-B	5½	major seventh
	C-Cb	5½		diminished octave
	C-B#	6		augmented seventh
	C-C	6	perfect octave

It’s very practical to be able to quickly recognize intervals. For that reason, I advice to do the exercises below.

Recommended exercises for note interval

Which interval is played on the piano (from C)?

Which interval is played on the piano (from any note)?