6

Where is middle C on the piano or keyboard?

You can watch this lesson in the video below, or read at your ease under the video.

From all the C’s on the piano, there’s only one that is the middle C. The middle C is, as you guessed already, a C that doesn’t sound (very) low nor (very) high. It sounds, well, in the middle… But where is middle C on a piano or keyboard? That depends on the piano or keyboard, as we will see later.

In the next sound sample, you can hear a middle C so you can compare it to the middle C on your piano or keyboard.

Where is the middle C?

The location of the middle C on a piano or keyboard depends on the number of keys that your instrument has. An acoustic piano normally has 88 keys. An electronic keyboard however has not necessarily always 88 keys. There are keyboards with 76, 73, 61 or 54 keys, and even other numbers of keys exist. As a general rule: the middle C is the C that is nearest to the exact middle of the keyboard.

Let me illustrate this with some keyboard-examples.

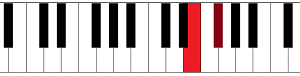
The middle C on an 88 key piano (most acoustic pianos)

To find the middle C on an 88 key piano or keyboard, look for the exact middle of the keyboard. Since the keyboard has 88 keys, this is between key 44 and 45 (red arrow in figure). The middle C (highlighted in blue) is the C nearest to the exact middle of the piano.

On an 88 key piano or keyboard, the middle C is the 4^th C from the left of the keyboard.

The middle C on a 76 key piano

The exact middle of a 76 key piano is showed in the next figure. In the same figure, the middle C –which is the C nearest to the middle of the keyboard- is also indicated.

The middle C on other keyboards

As mentioned above, the general rule states: the middle C is the C that is nearest to the exact middle of the keyboard. And, to be honest, it’s normally not even necessary to count the number of keys, divide by 2, look for the nearest C, etcetera: with a little bit of feeling, you can see at a glance which C is the middle C.

Please tell us what you think of this lesson by leaving a comment below.

4

Characteristics of intervals – Inversions

You can watch this lesson in the video below, or read at your ease under the video.

Inversions

Let me start with the example of the perfect 5^th interval from C to G, as indicated on the next keyboard:

You can make an inversion of this perfect 5^th interval by either taking the highest note and move it an octave down, or by taking the lowest note and move it an octave up. In the keyboard below, you see the highest note that was moved an octave down. Whether you move the highest note an octave down, or the lowest note an octave up, the result is the same: the inversion of the perfect 5^th interval from C to G is a perfect 4^th interval from G to C.

So, a perfect 4^th interval is the inversion of a perfect 5^th interval. The reverse is also true: a perfect 5^th interval is the inversion of a perfect 4^th interval. Together they add up to an octave, because a perfect 5^th (7 semitones) plus a perfect 4^th (5 semitones) make together 12 semitones, an octave.

You can also see it the following way: when you want to go from C to G, you can either go up a 5^th, or go down a 4^th.

Inversions of other intervals

Now, this is not only true for the ‘perfect 5^th-perfect 4^th pair’. Other pairs of intervals exist that act the same way. In fact, every interval has its inversion. For example, the inversion of the major 3^rd interval from –let’s say- E to G# is the minor 6^th interval from G# to E. Also here, the intervals add up to an octave, because 4 semitones (major 3^rd) plus 8 semitones (minor 6^th) equals 12 semitones (an octave).

A special case is the tritone interval. The tritone doesn’t need a partner, it just needs itself! A tritone splits an octave exactly in two equal parts, so a tritone just needs another tritone to make an octave.

A tritone consists of 6 semitones, so: 6+6=12, an octave!

Here’s a list of intervals with their inversions:

Intervals with their inversion:

Perfect unison + perfect octave   Semitone (or minor second) + major seventh Whole tone (or major second) + minor seventh Minor third + major sixth Major third + minor sixth Perfect fourth + perfect fifth Tritone + tritone

Notice that a perfect interval always goes together with another perfect interval and a minor interval always goes together with a major interval (and, of course, vice versa).

Please leave a comment below and tell us what you think of this lesson.

1

Note interval | Minor and Major Intervals | Intervals

You can watch this lesson in the video below, or read at your ease under the video.

When you play 2 different notes at the same time or one after the other, you will have a lower and a higher note. This means there is a distance (in pitch) between the 2 notes. This distance is called the interval between the 2 notes, the note interval, or simply interval.

You can measure this intervals between notes in number of semitones, and this takes us directly to our first interval: the semitone.

The semitone

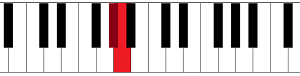
The easiest way to explain semitones is to look at the piano keyboard. A semitone is the interval from a key on the keyboard to the first note at the left or the right. So, for example, the interval from C to C# (or Db) in the next figure is a semitone.

Or, for example from G# (or Ab) to A:

It’s also possible to have a semitone between 2 white keys; this is the case between E and F and between B and C:

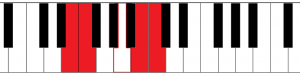
Notice that it’s not possible to have an interval of a semitone between 2 black keys on the piano.

Other names for a semitone are: half tone or half step.

The whole tone

The whole tone, or also called whole step, is an interval that consists of 2 semitones. Here are some examples of a whole tone:

From C to D:

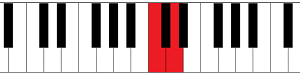
From F# (or Gb) to G# (or Ab):

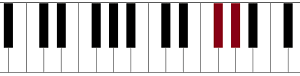
From E to F# (or Gb):

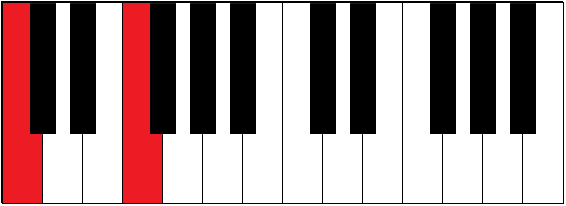
From Bb (or A#) to C:

 

Intervals from C to other ‘white key-notes’

Let’s take a look at the intervals from C to the other white keys on the piano up till the next C. Those notes are the notes from the C major scale (as you will learn later).

• When we call C the first note, D the second note, E the third note and so on, then the interval from C to the second note (D) is simply called ‘second’. The interval from C to the third note (E) is called ‘third’. And so on…
• The interval from C to the eighth note (C) is not called ‘eighth’, but ‘octave’.
• The interval from C to itself is called ‘’unison’.

In the table below, you can see an overview of all those intervals:

Note 1: the interval from C to D is not called ‘whole tone’ in this table, because ‘whole tone’ is actually an alternative name, where ‘second’ is more an official name. However, ‘whole tone’ is used more often than ‘second’.

Note 2: it might seem strange to call the unison an interval, since there is no distance between a note and itself. You could however call this a distance of 0 (semitones).

Interval on piano keyboard:	Interval between the notes:	Distance in (whole) tones:	Name of the interval:
	C-C	0	unison
	C-D	1	second
	C-E	2	third
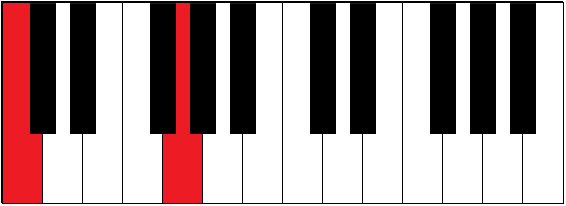
	C-F	2½	fourth
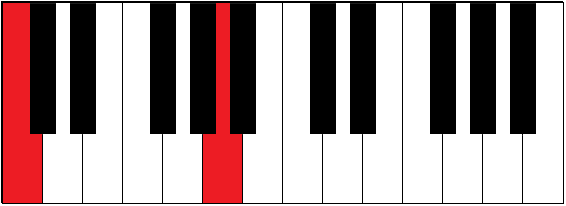
	C-G	3½	fifth
	C-A	4½	sixth
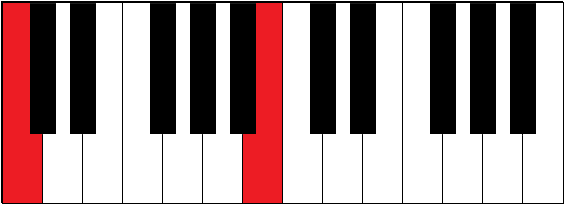	C-B	5½	seventh
	C-C	6	octave

 

All the intervals from C

Let’s also include in the table the intervals from C to the notes on black keys on the piano.

To do so, we have to introduce perfect intervals, major intervals and minor intervals.

Actually, in the table above, the unison, the fourth, the fifth and the octave are all perfect intervals. So, we speak of the perfect unison, the perfect fourth, and so on (even if we often omit the term ‘perfect’, and we just say unison, fourth, … etcetera).

All the other intervals in the table above are major intervals, so: major second, major third, major sixth and major seventh. The minor intervals will appear between C and the ‘black notes’ (table below).

In order to complete the table below, we have to follow the next rules:

• When a major interval is reduced by a half tone, it becomes a minor interval (this is not possible for a perfect interval). For example, when a major 3^rd interval (C-E) is reduced by a half tone, it becomes a minor 3^rd interval (C-Eb).
• Perfect intervals and minor intervals can be reduced by a half tone, they then become diminished intervals. For example, when a perfect 5^th (C-G) is reduced by a half tone, it becomes a diminished 5^th (C-Gb).
• Perfect intervals and major intervals can be increased by a half tone, they then become augmented intervals. For example, when a perfect 5^th (C-G) is increased by a half tone, it becomes an augmented 5^th (C-G#).

The table below can be scrolled horizontally (under the table).

Interval on piano keyboard:	Interval between the notes:	Distance in number of (whole) tones	Interval name (perfect/major/minor):	Interval name (diminished/ augmented):	Alternative name(s):
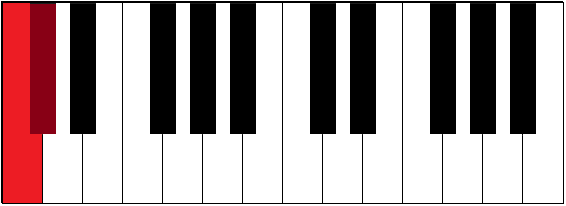
	C-C	0	perfect unison
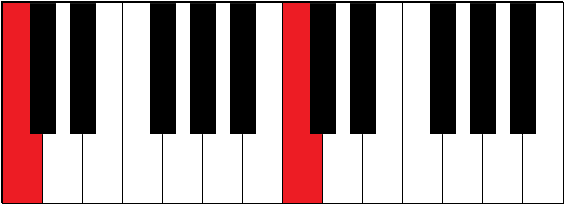
	C-C#	½		augmented unison	half tone, semitone, half step
	C-Db	½	minor second		half tone, semitone, half step
	C-D	1	major second		whole tone, whole step
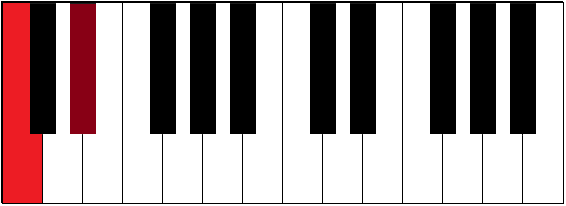	C-D#	1½		augmented second
	C-Eb	1½	minor third
	C-E	2	major third
	C-F	2½	perfect fourth
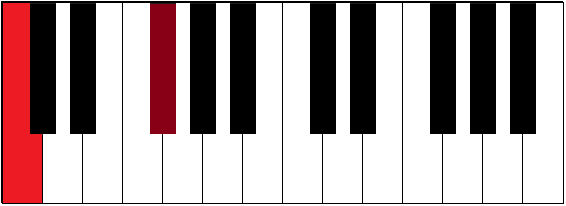	C-F#	3		augmented fourth	tritone
	C-Gb	3		diminished fifth	tritone
	C-G	3½	perfect fifth
	C-G#	4		augmented fifth
	C-Ab	4	minor sixth
	C-A	4½	major sixth
	C-A#	5		augmented sixth
	C-Bb	5	minor seventh
	C-B	5½	major seventh
	C-C	6	perfect octave

Now, I can imagine that all this looks quite difficult, especially when you’re a beginner and you see all those interval names for the first time.

In that case: don’t worry: we will, especially in the beginning, not use all those interval names. So don’t start learning the table above by heart, but limit yourself to the next intervals:

• Half tone (also called: semitone or half step)
• Whole tone
• Minor 3^rd
• Major 3^rd
• Perfect 4^th
• Perfect 5^th
• Major 6^th
• Minor 7^th
• Major 7^th
• Perfect octave

And, as I said before, I normally speak of the 4^th, 5^th and octave and not of perfect 4^th, perfect 5^th and perfect octave.

When you start learning about diminished chords, you should also know what a diminished 5^th and a diminished 7^th is, but that’s for later…

Note: We normally call the notes after their interval they make with the root (the root is the starting note, in our example the root is the note C (you will learn more about this in the major scales)). So, when the root is C, then the note E is called the major 3^rd. So, ‘major 3^rd’ is then not only the name of the interval (from C to E), but also of the note E (but only when the root is C!).

Intervals from another root note than C

Till now, we’ve only seen the intervals in the C major scale, so intervals from the root note C. How does this work in other major scales, or said in another way: how does this work from another root note than C?

Let me take as an example the root note G. So, we’re then looking for all the intervals from G to other (white and black) notes up till the next G an octave higher.

When you already know how major scales ‘work’, you can simply look at the G major scale: from G to the second note of the G major scale (A) is the major 2^nd, from G to the third note of the G major scale the major 3^rd, to the fourth note the perfect 4^th, and so on… Watch out: the major 7^th is now on a black key, the F#.

When you still don’t know how major scales ‘work’, then just look at the number of tones in the second table and apply that from the note G.

The result is shown in the table below:

The table below can be scrolled horizontally (under the table).

Interval on the piano keyboard:	Interval between the notes:	Distance in number of (whole) tones:	Interval name (perfect/major/minor):	Interval name (diminished/ augmented):	Alternative name:
	G-G	0	perfect unison
	G-G#	½		augmented unison	half tone, semitone, half step
	G-Ab	½	minor second		half tone, semitone, half step
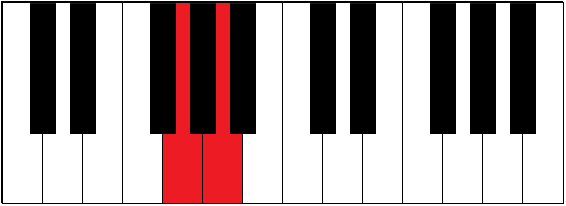	G-A	1	major second		whole tone, whole step
	G-A#	1½		augmented second
	G-Bb	1½	minor third
	G-B	2	major third
	G-C	2½	perfect fourth
	G-C#	3		augmented fourth	tritone
	G-Db	3		diminished fifth	tritone
	G-D	3½	perfect fifth
	G-D#	4
	G-Eb	4	minor sixth
	G-E	4½	major sixth
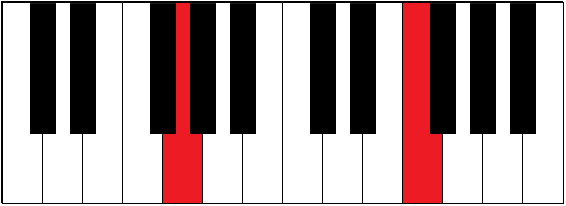	G-E#	5		augmented sixth
	G-F	5	minor seventh
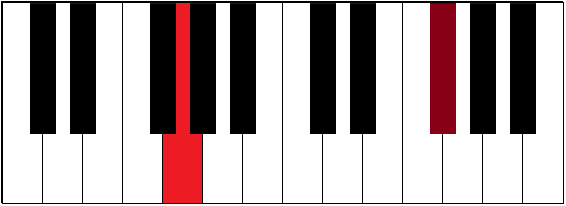	G-F#	5½	major seventh
	G-G	6	perfect octave

One further step

When you’re already more advanced in music (theory) and you want to know more about intervals, then keep reading. When you’re a beginner, then just scroll down to the bottom of this page where you will find interactive exercises about intervals.

In the first lesson (about note names) I told you already something about double sharps and double flats.

As you know, C and Dbb are the same note on the piano. Does this mean that the interval between C and Dbb is the same interval as the interval between C and C, so a unison?

No. The interval from C to Dbb is not called a unison. We call this interval a diminished 2^nd.

But why second? This is because Dbb is based on the note D: it is a D that has been lowered twice by a half tone: From C to D is a major 2^nd, from C to Db a minor 2^nd, so from C to Dbb a diminished 2^nd.

Now, to be honest: you will almost never see the name ‘diminished 2^nd’, but officially it exists.

But, for example a diminished 7^th occurs often in music, for example in the C diminished chord. A diminished 7^th is a half tone lower than a minor 7^th, so a half tone lower than Bb (when C is the root note). This makes the diminished 7^th in the key of C the note Bbb, which is on the piano the same note as the A.

We can now extend our table as follows (from the root C):

The table below can be scrolled horizontally (under the table).

Interval on the piano keyboard:	Interval between the notes:	Distance in number of (whole) tones:	Interval name (perfect/major/minor):	Interval name (diminished/ augmented):	Alternative name:
	C-C	0	perfect unison
	C-Dbb	0		diminished second
	C-C#	½		augmented unison	half tone, semitone, half step
	C-Db	½	minor second		half tone, semitone, half step
	C-D	1	major second		whole tone, whole step
	C-Ebb	1		diminished third	whole tone, whole step
	C-D#	1½		augmented second
	C-Eb	1½	minor third
	C-E	2	major third
	C-Fb	2		diminished fourth
	C-E#	2½		augmented third
	C-F	2½	perfect fourth
	C-F#	3		augmented fourth	tritone
	C-Gb	3		diminished fifth	tritone
	C-G	3½	perfect fifth
	C-Abb	3½		diminished sixth
	C-G#	4		augmented fifth
	C-Ab	4	minor sixth
	C-A	4½	major sixth
	C-Bbb	4½		diminished seventh
	C-A#	5		augmented sixth
	C-Bb	5	minor seventh
	C-B	5½	major seventh
	C-Cb	5½		diminished octave
	C-B#	6		augmented seventh
	C-C	6	perfect octave

It’s very practical to be able to quickly recognize intervals. For that reason, I advice to do the exercises below.

Recommended exercises for note interval

Which interval is played on the piano (from C)?

Which interval is played on the piano (from any note)?

0

The note names and how to find the notes on a piano keyboard

You can watch this lesson in the video below, or read at your ease under the video.

What are the music note names used in Western music?

In Western music, we can distinguish 12 different notes. Every song or piece of music is made of only those 12 different notes.

The easiest way to show the 12 notes is on a piano keyboard. On the keyboard, you can see a repetitive pattern of white and black keys.

One such a pattern consists of 12 keys,

7 white keys:

and 5 black keys:

Those are exactly the 12 different notes in Western music we spoke of above.

The note names of the white keys

This might sound funny, but to find the names of the white keys, look first at the black keys: they come in groups of 2 black keys and 3 black keys. Just at the left of a group of 2 black keys you can find the note C.

To find the names of the other white keys, just go up alphabetically to G as in the next figure.

Now, we have to name 2 more white keys. Notice that we’ve used the letters C to G in alphabetical order, but we haven’t used the 2 first letters of the alphabet yet. So, let’s use them for the 2 missing keys, as follows:

The note names of the black keys

Do you remember that we had to look at the black keys first to find the names of the white keys? Well, let’s reverse the roles now: to find the names of the black keys, we have to look at the white key names first, since the names of the black keys are derived from the white key names.

As you can see, a black key is always situated between 2 white keys. The black key indicated by the arrow in the figure below is for example between the C and the D. As this note is higher than the C, but lower than the D (the pitch of the notes gets higher when you go from left to right), we call this note C sharp, or D flat.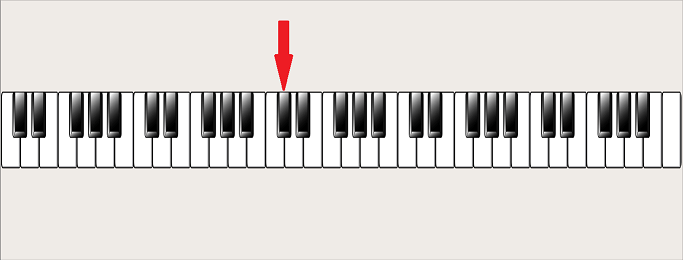 So, sharp means: the note just at the right, and flat means: the note just at the left. We write C sharp as C# and D flat as Db.

So the black keys actually have 2 names, the name of the white key at the left with a sharp (#) sign, or the name of the white key at the right with a flat (b) sign.

In the next figure, you can see all the names of the notes on a piano keyboard.

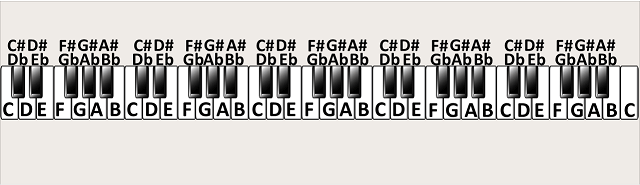
As you can see, this is a pattern of 12 different notes (represented on the piano by 7 white keys and 5 black keys) that repeats itself.

Double sharps and double flats

Btw, notice that on the right side of the B and on the right side of the E, there is no black key. So you could call the C also B#, and the F an E#. Or, in the same way, you could call the B a Cb and the E an Fb. In music theory, this is sometimes needed (the 7^th note in the F# major scale is an E#, not an F, even if it is exactly the same note). It is even possible to have double flats (bb) or double sharps (##). For example, a C## is raised 2 times, so this is equivalent to a D. A shorter writing for double sharp looks a bit like an x (see figure below), so Cx would be the same note as C## or just simply D.

Enharmonic equivalent

Two notes that are written differently, but that are actually one and the same note, are called enharmonic equivalent notes.

C# and Db are for example enharmonic equivalent notes: they are written differently, but are the same note.

Other examples:

• A# and Bb
• E# and F
• F## (or Fx) and G
• Bbb and A
• etcetera

After this lesson, you should be able to recognize the keys of the piano and know the names of the corresponding notes. In the beginning, you will probably not remember every note and every key on the piano, so just practice 5 minutes a day and you will see: in no time you will master it.

The exercises that are accesible via the links below will certainly help you to practice the notes.

Recommended exercises for music note names

Which note is played on the piano?

Place the note on the right key of the piano

Did you already know the note names and/or the corresponding keys on the piano? Did this lesson help you to learn the notes and keys on the piano? If so, please leave a comment below.